|
 |
|||||
|
|
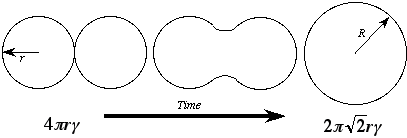
Background Consider two copper rods, each of radius r, touching at a temperature such that diffusion is reasonably rapid (see Fig. 1). The total free energy of the system can be characterized by the volume free energy of each rod, DGv, and the surface free energy of each rod, g. Per unit length of rod, the total free energy of the pair of rods is:
If the two rods were to be combined into one rod of cross section 2 pR2 (it can be shown by volume conservation that the new radius is R =
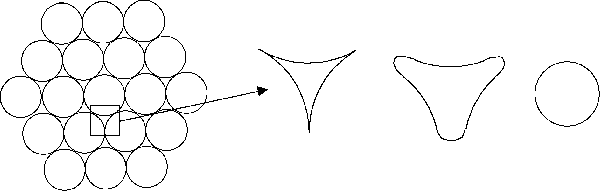
Figure 1. Schematic representation of surface energy driven shape changes. However, we can use a modified version of this experiment to illustrate the principle and to show the basis for the important processing technique known as sintering. Consider a collection of identical rods arranged in a close-packed configuration. If we can eliminate the near-triangular voids, we can reduce the surface energy and hence the total free energy of the system. There are some important, but difficult, concepts in discussing the detailed mechanisms by which this occurs so we will substitute a simple rule which serves to illustrate the intermediate stages (and happens to be correct). This rule says that surfaces move toward their center of curvature. Thus, the triangle goes through the stages illustrated in Fig. 2 until the free space is eliminated and densification has resulted.
Figure 2. Shape evolution of the pores between the Cu wire. These shapes are schematic, and the volume decrease with time is not shown. We can think of the free space between wires as being a collection of vacancies and the disappearance of this space as the result of these vacancies "dissolving" in the metal. Since at a given temperatures and pressures, only a very small number of vacancies is in equilibrium with the lattice, the extra defects must disappear permanently at "sinks". By far, the most effective sinks are large-angle grain boundaries where a vacancy can disappear in the poorly packed layers between the grains. Thus, we would expect the rate of sintering to depend on grain size (the mean distance to a sink). We will study the reduction of surface area in an array of copper wires which are heated to a temperature sufficiently high that diffusion can cause mass transfer. The net result is densification and, for other reasons, grain growth in the copper (which may affect the rate of the reaction since it is largely these boundaries which consume the diffusing vacancies). |
||||
|
|
|||||