|
 |
|||||
|
|
Background
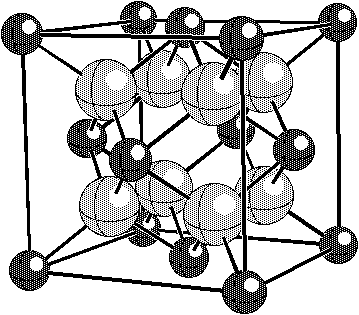
As an example of how the charge compensating defect mechanism can be identified, we consider the well- known example of the dissolution of CaO in ZrO2. This system has some parallels with the Bi2O3•Nb2O5 system. For example, small amounts of CaO stabilize the cubic fluorite structure. The fluorite structure, illustrated in Fig. 1, takes space group Figure 1. In the fluorite structure, the cations (smaller, darker atoms) occupy the ccp positions and the oxygen ions occupy the tetrahedral sites. In the We will consider two possible defect models for the CaO•ZrO2 system: charge compensation by oxygen vacancies and charge compensation by Zr interstitials.
Solid solutions produced by these different reactions will have different densities. To find the density for each one, we imagine a solid solution between the defective structure and ideal structure. So, we have to find the molecular weight of the defective formula unit. For reaction (1), the defective formula unit is made up of one Ca, one O, and one vacancy. For reaction (2), the defective formula unit is made up of one Ca, two O, and one half of a Zr (in an interstitial site. So, the formula weight for each solid solution is:
where MCaO, MCaO2, MZrO2, and MZr are the molecular weights of CaO, CaO2, ZrO2, and Zr, respectively. To calculate the density, we must note that there are 4 formula units per cell and know the lattice parameter. Thus, we have the equation:
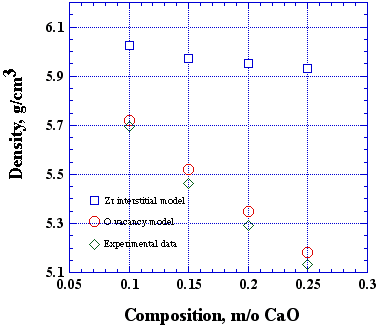
Where Z is the number of formula units per unit cell, x is the composition, M is the mass, V is the unit cell volume, and N is Avegadro's number. If you take x = 0.15, Z = 4, and the cubic lattice constant of 5.1535 Å, we calculate densities of 5.52 and 5.92 g/cm3 for the vacancy an interstitial models, respectively. Thus, the two hypothetical models predict a 8% difference in the density. Assuming that mass and volume measurements can be made with this accuracy, then it is possible to distinguish these models. The results of Diness and Roy [A. Diness and R. Roy, "Experimental confirmation of major change of defect type with temperature an composition in ionic compounds," Solid State Commun. 3 [6] (1965) 123-125.], who originally conducted this experiment, are shown in Fig. 2.
Figure 2. Summary of results from the CaO•ZrO2 system. The data support the oxygen vacancy model given by reaction 1. From: A. Diness and R. Roy, "Experimental confirmation of major change of defect type with temperature an composition in ionic compounds," Solid State Commun. 3 [6] (1965) 123-125. Pychnometric density measurements can be made in a number of ways. Perhaps the easiest way is to use Archimedes principle: that a body wholly or partly immersed in a fluid is bouyed up with a force equal to the weight of the fluid displaced by the body. So, if wi is the weight of the specimen immersed in fluid, then wi is the difference between the true specimen weight (ws = rsVsg) and the weight of the displaced fluid (wf = rfVfg):
If we also consider the weight of the specimen in air:
Noting that all of the volumes are the same and that the true specimen weight and the weight in air are about the same,
So, if you measure the weight in air and in a fluid of known density, it is possible to calculate the density of the specimen. A pychnometer works by using two chambers of known volume. The reference volumn (Vr) is filled to a known pressure (P1) above ambient. The ideal gas law then relates the pressure and volume to the ambient temperature (Ta) and the moles of gas (n1) in the volume.
Similary, the volume of gas in the test cell is the cell volume (Vc) minus the volume of the powder (Vp). At ambient presure (Pa) we have:
Where na are the moles of gas in the test cell. When the valve connecting the two chambers is open, the reference pressure decreases and the pressure in the test cell increase to P2:
Substituting the right hand sides of the two previous equations, you have:
Since the instrument is zeroed so that the ambient pressure is 0,
So, by knowing the test cell volume and the reference volume, and by measuring the pressure before and after the valve between them is open, the volume of the power cen be measured. By weighing the sample, one can then determine the density.
|
||||
|
|
|||||
(no. 225), has four CaF2 formula units per cell, and situates that Ca in 4a positions (0,0,0 +F) and the O in 8c positions (1/4,1/4,1/4; 1/4,1/4,3/4 +F).
(1)
(2)
, vacancy reaction
, interstitial reaction
.
.
,
.
,
